El resumen del presente artículo (Carol Matthews, Zeena Farook & Peter Helm) proporciona una visión general del documento técnico sobre el análisis de estabilidad de taludes, comparando los métodos de equilibrio límite y de elementos finitos, y destaca los resultados y conclusiones clave de varios estudios de caso. Como se conoce, desde 1930, el enfoque de equilibrio límite (LE) se ha utilizado para analizar la estabilidad de taludes. Este método ha evolucionado desde el método de círculo sueco de Fellenius hasta métodos más avanzados como el de Bishop, que mejoran la precisión del factor de seguridad (FoS). Con el avance de la tecnología, el método de elementos finitos (FE) ha ganado popularidad, ofreciendo una mayor precisión en la modelación de geometrías complejas y comportamientos del suelo.

• Se basa en dividir el talud en finas secciones y aplicar ecuaciones de equilibrio de fuerzas y momentos.
• Métodos comunes incluyen los de Fellenius y Bishop, siendo este último más preciso.
• La simplicidad y la precisión del método LE lo hacen ampliamente utilizado.

• Permite modelar taludes con alta precisión, incluyendo geometrías complejas y secuencias de carga.
• Usa el método de reducción de resistencia, reduciendo la cohesión y el ángulo de fricción del suelo hasta que falla.
• Proporciona una mejor visualización de las deformaciones del suelo.

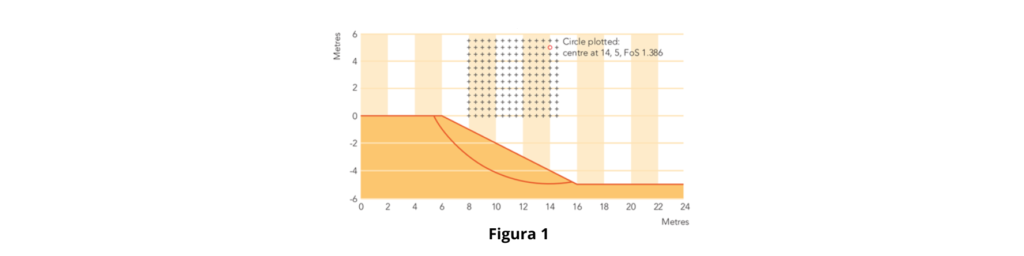
Este ejemplo, basado en el artículo de Griffiths y Lane (1999), corresponde a un talud homogéneo con talud de 1V:2H con un estrato subyacente de alta resistencia y rigidez. El ángulo de fricción interna del suelo es de 20° y la cohesión es proporcional al peso unitario del suelo y la altura del terraplén. Ver Figura 1.

• Se compararon los métodos LE y FE usando datos de proyectos reales.
• Los resultados mostraron que ambos métodos proporcionan factores de seguridad similares, aunque el método FE ofrece una mayor precisión en la identificación de superficies de falla.

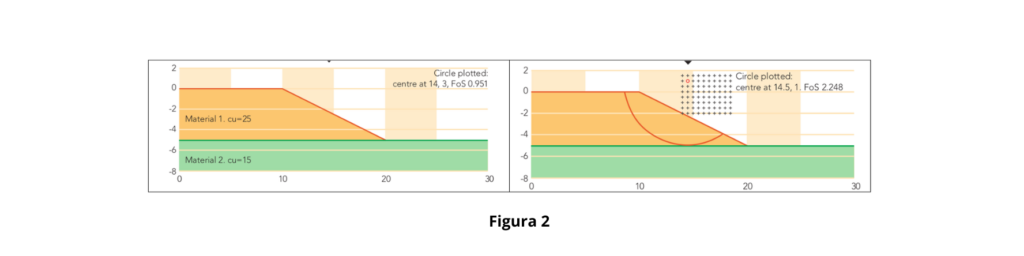
Este ejemplo modela un talud homogéneo con talud 1V: 2H, capas horizontales. El ángulo de fricción interna del suelo es de 20° y la cohesión es proporcional al peso unitario del suelo y la altura del terraplén. La geometría se muestra en la Figura 2 que corresponde al ejemplo 4 del artículo de Griffiths y Lane (1999).

• Se analizó un talud con un estrato de cimentación con diferente cohesión.
• El método FE mostró ventajas en la identificación de mecanismos de falla profunda y superficial simultáneamente, algo que el método LE podría pasar por alto.

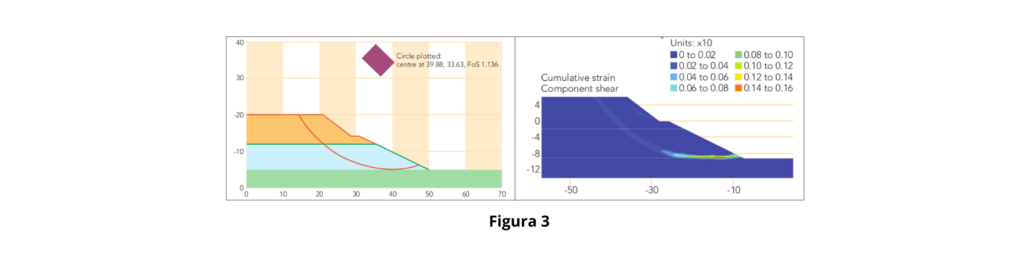
• En este ejemplo (tomado de Chowdhury y Xu, 2005) se modela un corte en múltiples estratos horizontales del suelo. Este ejemplo es una simplificación basada en un fallo de corte real. Los análisis de estabilidad del problema se pueden ver en la Figura 3.
• Se modeló un corte en múltiples estratos horizontales, basado en un fallo real.
• Ambos métodos mostraron buenos resultados, pero el FE identificó una segunda superficie de falla que el LE no detectó inicialmente.

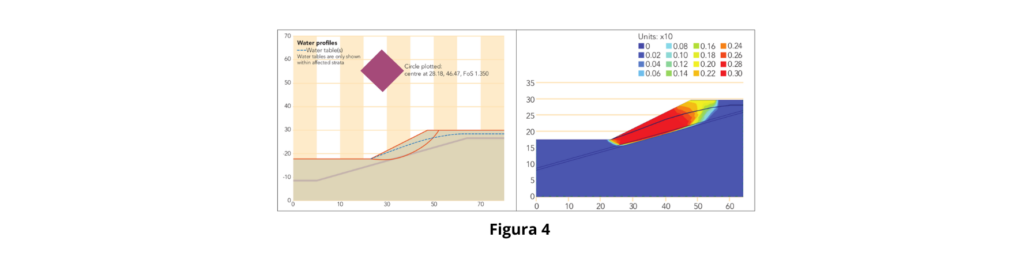
• Este problema es una variación de un ejemplo proporcionado por Giam y Donald (1989) con un talud con pendiente pronunciada que incorpora una capa de suelo débil y delgada, y con nivel freático variable.
• El análisis mostró que el método FE es más adecuado para taludes con estratigrafías complejas y capas de suelo de diferentes propiedades.
• El método FE proporcionó un FoS más bajo y una mejor identificación de la geometría de la superficie de falla.

• Ambos métodos, LE y FE, tienen sus ventajas y desventajas.
• El método LE es adecuado para problemas simples y proporciona resultados fiables de manera eficiente.
• El método FE es más adecuado para problemas complejos con geometrías y comportamientos del suelo complicados.
• La elección del método depende de la complejidad del problema y de la precisión requerida.

(*) Artículo Técnico. Análisis de estabilidad de taludes: Límite Equilibrio o Método de Elementos Finitos. Carol Matthews, Zeena Farook & Peter Helm. 2014.